Multi-tenor swap surface and dual curve pricing

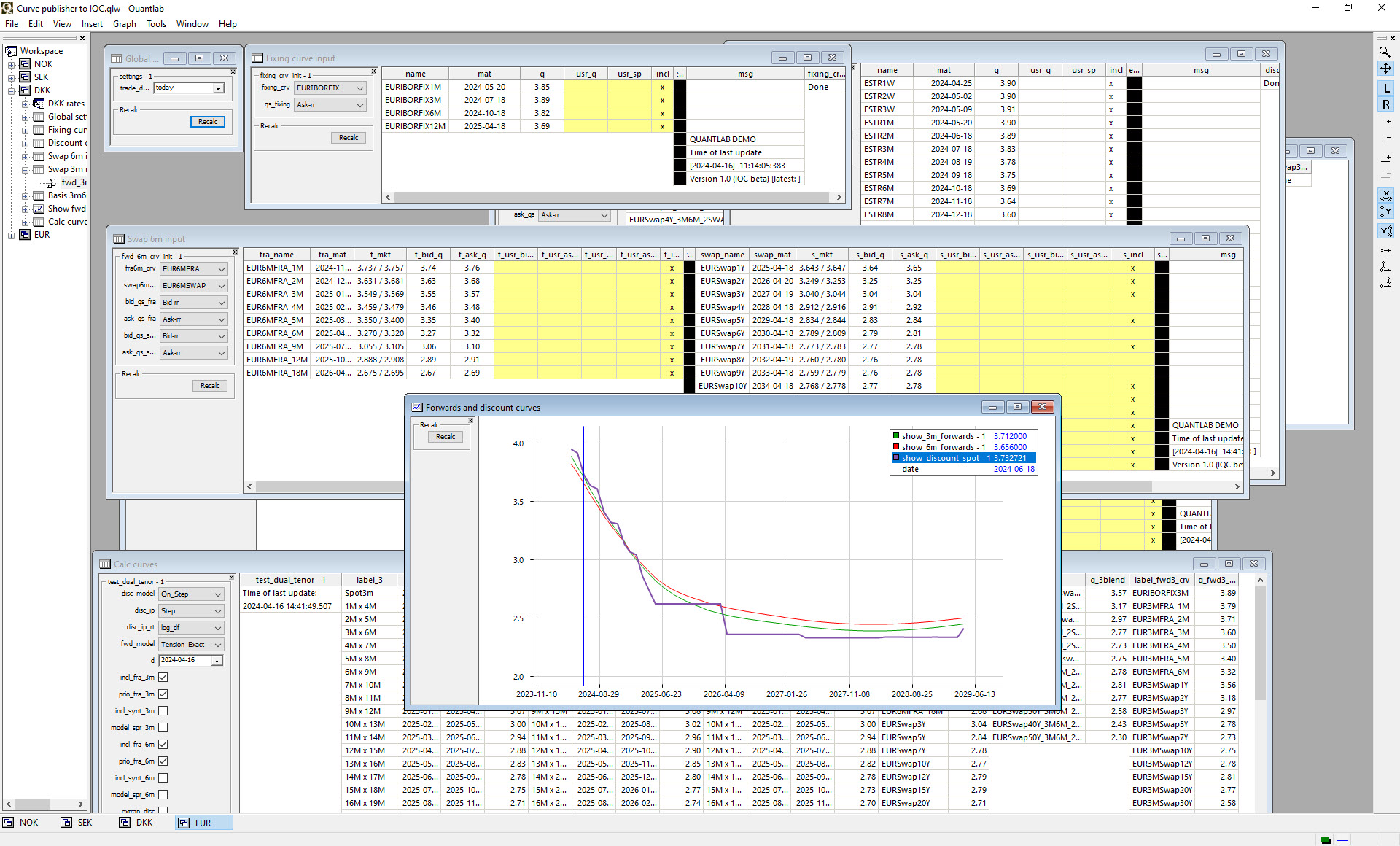
In the post credit crisis swap market the curve building process has completely changed and what was before a fairly straightforward procedure is now a lot more involved. Why is that? Tenor basis spreads are now large while before they were close to zero meaning that we now need to build curves that are homogeneous in the underlying rate tenor. It is also necessary to have a unique discounting curve for all tenor curves and the discounting curve is now commonly, for collateralized derivative deals, the ois curve. In other words, the forecasting curve is now separate from the discounting curve. For each currency we can think of all the different libor instruments as giving us a surface more than a curve.

The impact of moving to ois discounting is not the same for all types of deals. The impact is low for recently traded (close to par) swaps and short dated options. The impact is high for older long dated swaps (off-market), zero coupons and long dated options.

I will illustrate how I use Quantlab to give me the individual curves, the surface and then apply dual-curve pricing to a swap. It is actually easy to do with Quantlab.

Here's the procedure from curve creation to pricing:

(1) build the discounting curve using for example a single curve bootstrapper modified to take into account the "step" behavior of rates between central bank meeting dates. The typical instruments here are ois swaps but should in principle depend on counterparty credit or funding of collateral.

(2) select vanilla instruments for each tenor curve i.e. each curve must have instruments that are homogeneous in the underlying rate (typically with 1M, 3M, 6M,12M tenors). The typical instruments here are FRA contracts, Futures, Swaps and Basis swaps.

(3) build the forward curves using the selected instruments using the libor instruments and the discounting curve.

(4) compute for each forward curve the forward rates and the corresponding cashflows relevant for pricing the derivative with the same underlying. Beware of odd periods which could mean that several tenors (possibly interpolated) are relevant for the pricing.

(5) calculate the present value of the derivative using the discounting curve and the cashflows.

‍