Credit crisis and dual curve construction using OIS
It has hardly escaped anyone that the credit crisis has forced the market to price in counterparty credit risk. Here we dive into "dual bootstrapping".
That it would have such a profound impact on simple things like standard pricing of a fixed/float interest rate swap is now clear. Everyone in the market is not on level playing field in terms of how this should be done however. The finance and mathematics behind a ”simple” yield curve fit is no longer to find in the university press text books.
That the Eonia/Estr has become the new market standard for discounting risk free flows is however now clearly evident. In this presentation we go through the basics of dual curve construction without getting into the formulas behind. We provide a some standard instruments pricing differences in the new and old model.
Inputs
1.A blended curve having instruments of equal tenor (ex 6M for EURSWAP market)
2.A discount curve matching the funding levels appropriate to the particular deal/ctpy. (Ex. OIS)
3.Short-end and long-end extrapolation. (I.e. No depos mixed with FRAs -> use synthetic instruments.)
4.Choice of fwd model / interpolation as well as discount model / interpolation.
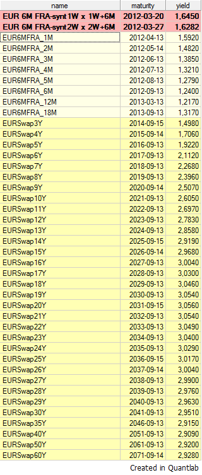
Forward curve instruments
•Using 6M FRA blended with
•EUR 6M SWAPs is one possibility
•Here the FRAs are prioritized.
•Please note. No depos.
Discount (funding) curve
•Overnight index swaps (OIS)
•Use tailored funding curve if CSA is used.
Two types of discount fit-models
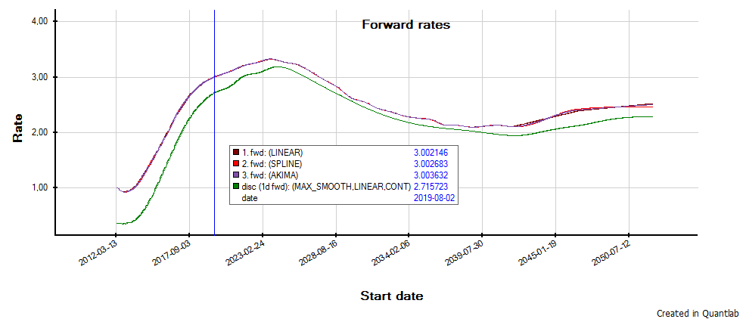
1. Exact fit such as Bootstrap which prices all instruments exactly. Here we have a choice of interpolation models on intermediate nodes such as:
Linear, Step, Spline, Hagan West, Hermite, Akima, with our without Hyman monotonicity filters. Step for bank meeting dates. Don't forget the turns.
2. Parametric or best-fit models such as Maximum-Smoothness, Tension-Splines, Taanggard, Nelson-Siegel etc.
Interpolate the discrete tenor forward curve
Linear, Step, Spline, Hermite, Akima, with our without Hyman monotonicity filters.
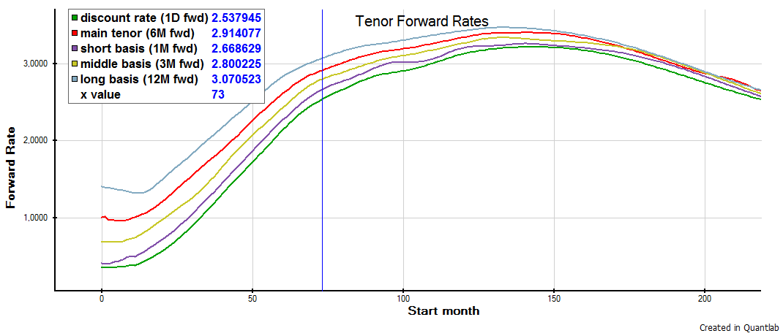
We now want to repeat the forward curve construction for all non-standard tenors such as the 1M, 3M, and 12M, interpolated on the discrete fwds.
In order to do so we also use the relevant basis spread curves.
We can now extend the non-standard curves using 1M Swaps on the 1M curve, 3M Futures on the 3M curve, 12M FRAs on the 12M curve etc.
Hopefully we now end up with a set of forward curves all created using the dual curve set-up and joint OIS discounting.
